Research
Causality
As an observational science, most studies in astrophysics relies on correlations. Indeed, the natural way of determining causation is through interventions, e.g. controlled experiments in labs. However, such interventions are impossible in astrophysics as humans have no control over the universe, thus most studies are limited to correlations.
This conundrum can be resolved by the field of causal discovery, a field that aims to infer causal relationships from observational data. This is accomplished mainly through examining the conditional independence relationships between variables, which can be represented by a causal graph.
I am working on bringing causality to astrophysics, with the aim to understand the causal relationships behind astro data.
One of my recent work tries to solve the long-standing debate about the causal interpretation of the correlations between the mass of central SMBHs and the properties of their host galaxies. Causal discovery algorithms are applied to real observational data.
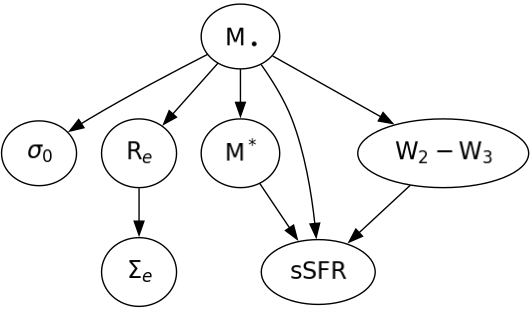
Example causal relationship identified in real spiral galaxy data shown in a directed acyclic graph (DAG).
The causal discovery is carried out in a Bayesian way, where we calculate exact posterior probabilities of every possible DAG given the data, $P(G \mid D)$. This enables us to give the probability of any causal relationship between variables of interest. We find distinct causal relationships for elliptical, lenticular, and spiral galaxies. Submitted to ApJ
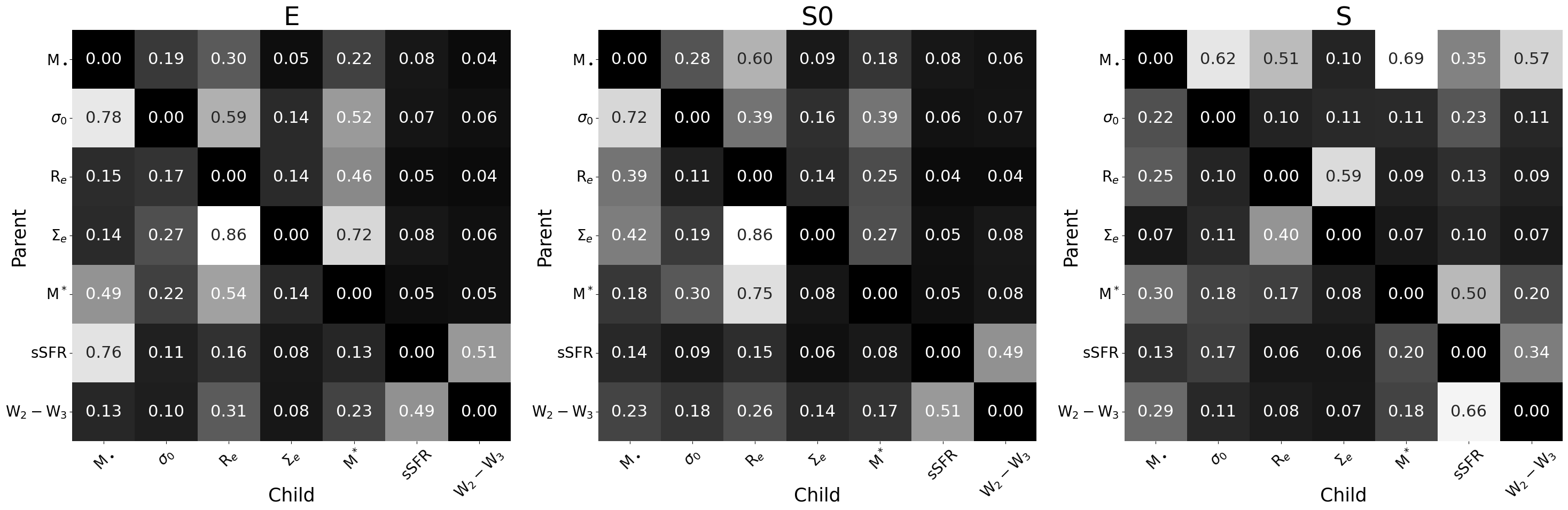
Exact posterior edge marginals for elliptical (E), lenticular (S0), and spiral (S) galaxies.
Edge marginals give the probability of Parent $\rightarrow$ Child through directed edges summed over all DAGs and their probabilities. E.g. in E galaxies the chance of $\sigma_0 \rightarrow M_\bullet$ is 78%.
Symbolic Regression
Symbolic regression is a machine learning technique that aims to find a mathematical expression that best fits the data. Based on Occam’s razor, which states that the simplest model that fits the data is the best model, SR finds a pareto front that best optimizes the trade-off between model complexity and accuracy.
There are many scaling relations in astrophysics, such as 2-D ones including the Tully-Fisher relation, the Faber-Jackson relation, and the M-sigma relation, or 3-D ones such as the fundamental plane of elliptical galaxies. Symbolic regression can be used to find new (higher dimensional) scaling relations and provide new insights into the astrophysical processes behind these relations.
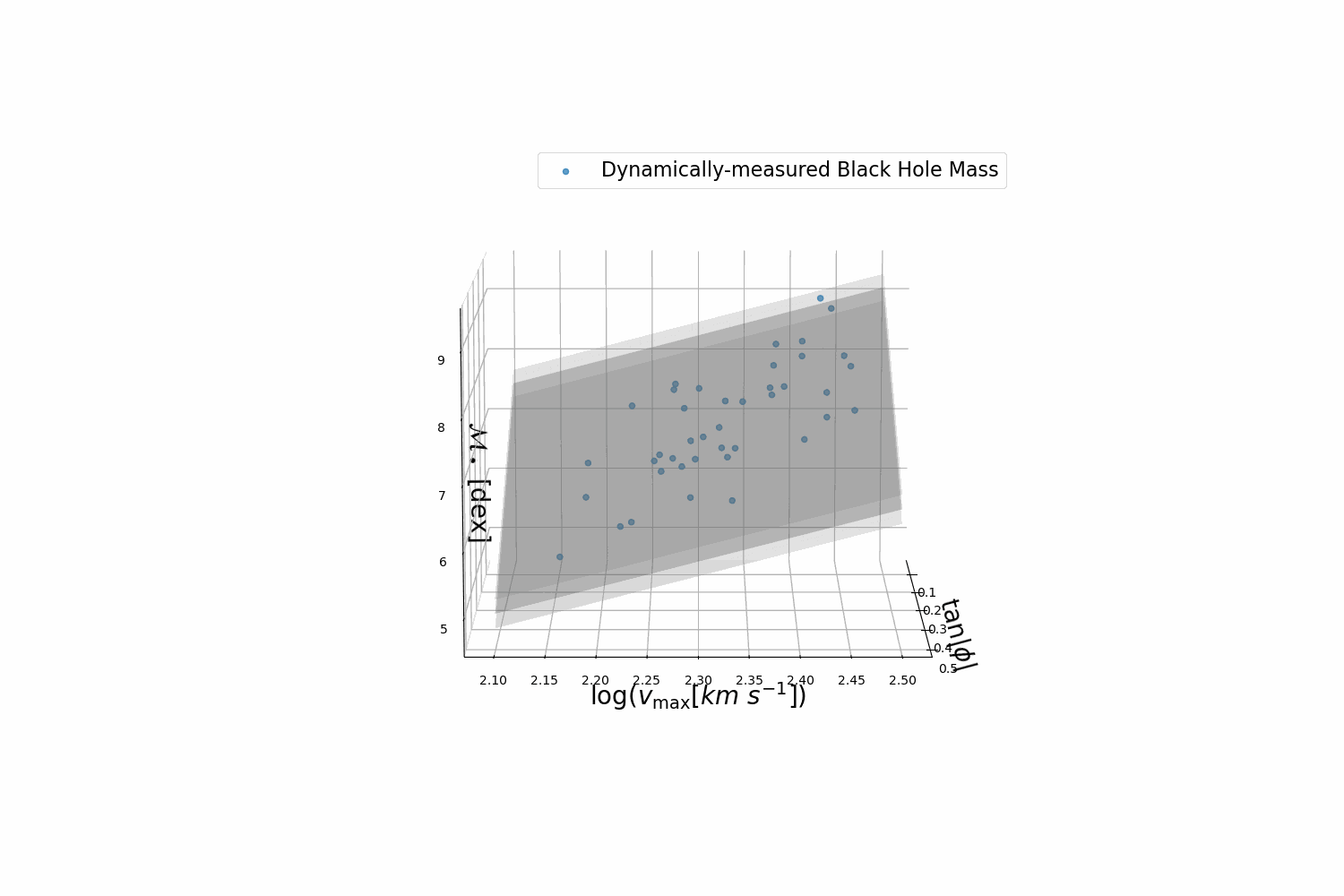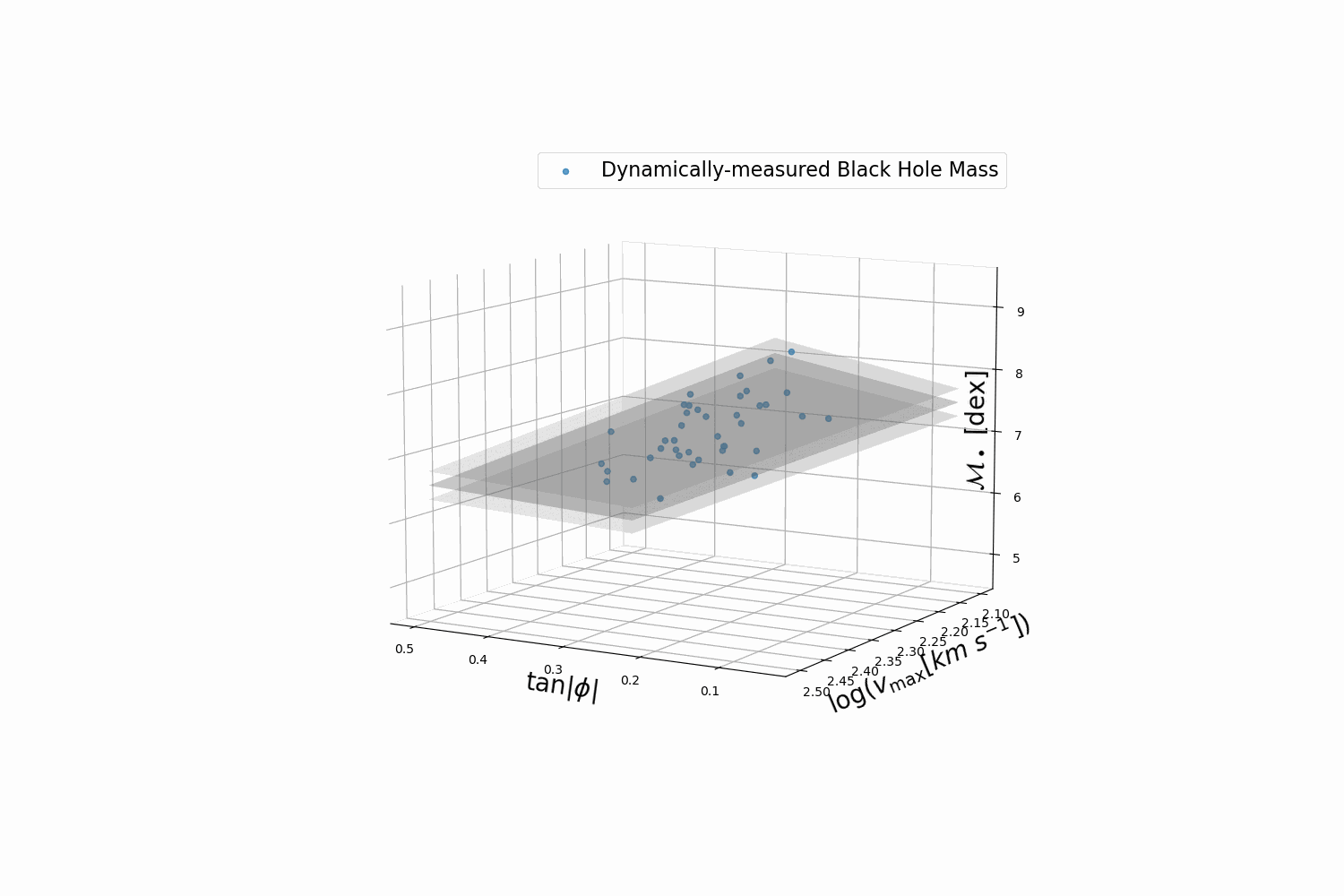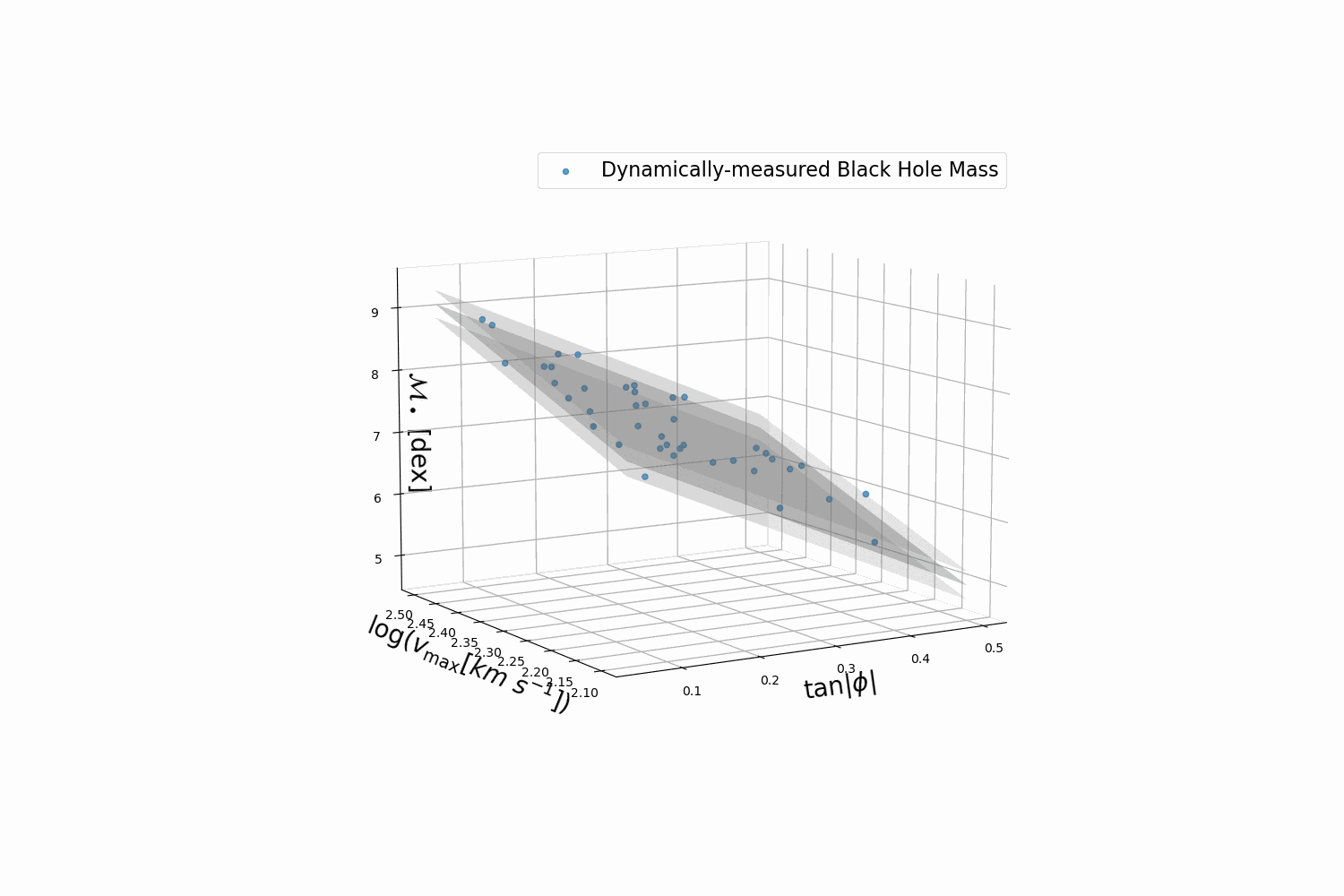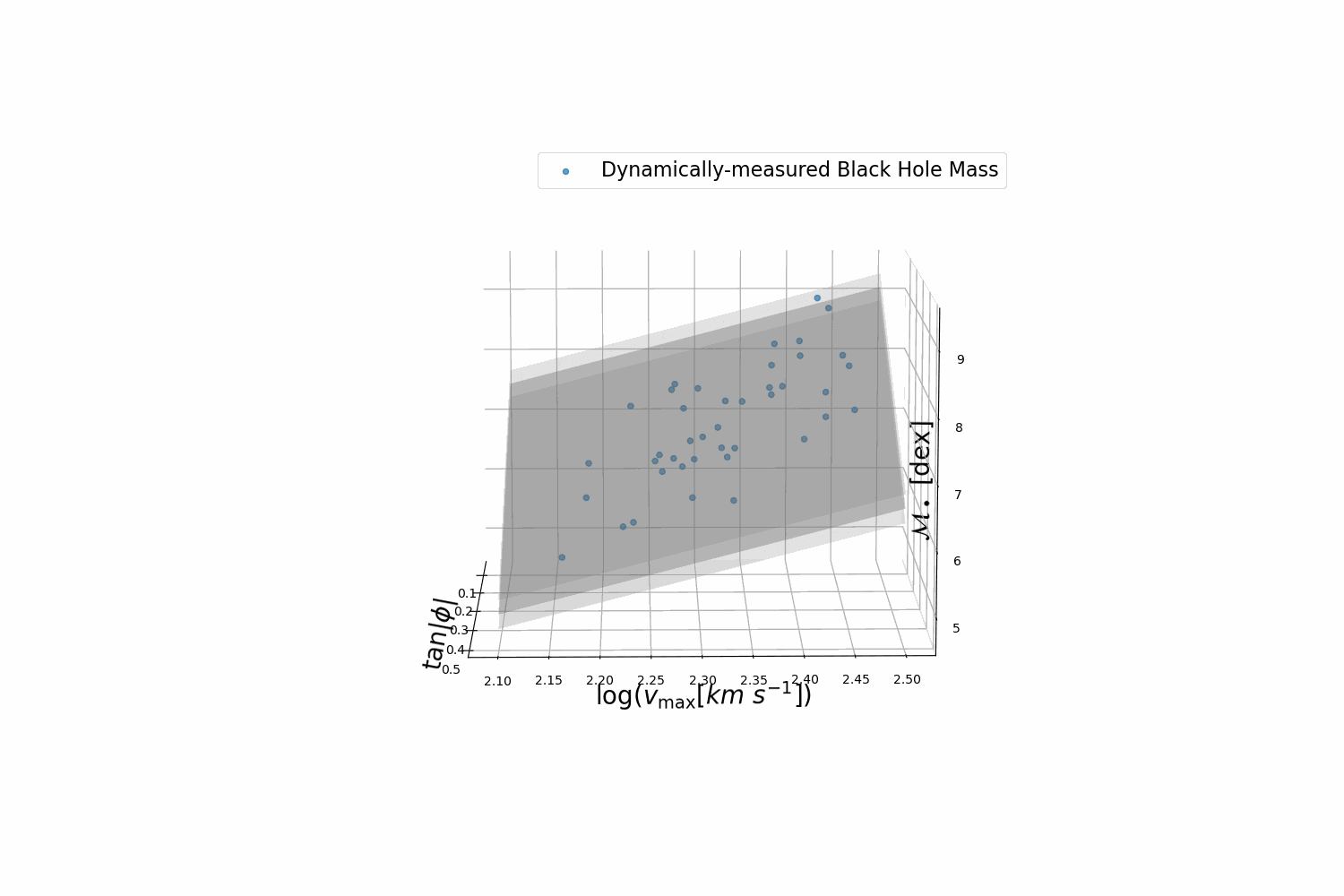 A $M_\bullet$-$\phi$-$v_{max}$ planar relation for spiral galaxies identified by Symbolic regression. Published in ApJL
A $M_\bullet$-$\phi$-$v_{max}$ planar relation for spiral galaxies identified by Symbolic regression. Published in ApJL
Symbolic regression can also be used to unveil the black-box of deep learning models, by condensing neural networks into human-readable mathematical expressions. This will help us understand the underlying physics behind the neural networks.
Simulations vs. Observations
I work in a group that is the home of NIHAO (Numerical Investigation of a Hundred Astrophysical Objects) simulations. NIHAO is a suite of cosmological zoom-in hydrodynamical simulations.


Gallery of NIHAO simulated galaxies.
I have a rich experience in analyzing these simulations and comparing them with observations. One of my projects uses anomaly detection to quantify the differences between real observed galaxies images and simulated galaxy images. Published in MNRAS